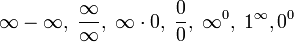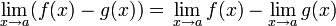limites de matematicas: agosto 2009

Indeterminaciones

Hay límites que evaluándolos directamente, se obtiene alguna de las siguientes expresiones:

$\infty - \infty, \; \frac{\infty}{\infty}, \; \infty \cdot 0 , \; \frac{0}{0}, \; \infty ^0, \; 1^\infty,0^0 \,$

A estas expresiones se les denomina indeterminaciones, ya que, a simple vista, no está claro cual puede ser el límite (si es que existe). En algunos casos, simplificando las expresiones u obteniendo expresiones equivalentes a las iniciales se puede resolver la indeterminación y calcular el límite. En otros casos, se requerirá el uso de otras herramientas más potentes como pueden ser desigualdades o la regla de L'Hopital.

Un ejemplo de indeterminación del tipo $\textstyle \frac{0}{0}$ es la que se da en estos tres casos, y en cada caso (tras simplificar), se obtiene un límite distinto :

$\lim_{t\rightarrow 0}\frac{t}{t^2}=\frac{0}{0} \quad \xrightarrow[\mathrm{simplificando}]{} \quad \lim_{t\rightarrow 0}\frac{1}{t} = \infty$

$\lim_{t\rightarrow 0}\frac{t}{t}=\frac{0}{0} \quad \xrightarrow[\mathrm{simplificando}]{} \quad \lim_{t\rightarrow 0} 1 =1$

$\lim_{t\rightarrow 0}\frac{t^2}{t}=\frac{0}{0} \quad \xrightarrow[\mathrm{simplificando}]{} \quad \lim_{t\rightarrow 0} {t} = 0$

propiedades de los limites

Propiedades de los límites

Generales

Los límites, como otros entes matemáticos, cumplen las siguientes propiedades generales, que son usadas muchas veces para simplificar el cálculo de los mismos.

$\lim_{x \to a} x = \, a \,$

Límite por un escalar.

$\lim_{x \to a} kf(x) =\, k\lim_{x \to a} f(x)\,$ donde k es un multiplicador escalar.

Límite de una suma.

$\lim_{x \to a} (f(x) + g(x)) =\, \lim_{x \to a} f(x) + \lim_{x \to a} g(x)\,$

Límite de una resta.

$\lim_{x \to a} (f(x) - g(x)) =\, \lim_{x \to a} f(x) - \lim_{x \to a} g(x)\,$

Límite de una multiplicación.

$\lim_{x \to a} (f(x) \cdot g(x)) =\, \lim_{x \to a} f(x) \cdot \lim_{x \to a} g(x)\,$

Límite de una división.

$\underset {x \to a} {\lim} \; \frac {f(x)}{g(x)} = \frac {\underset {x \to a} {\lim} \; f(x)} {\underset {x \to a} {\lim} \; g(x)} \quad \mathrm{si}\ g(x) \ne 0$

limite de una funcion

El límite de una función es un concepto fundamental del cálculo diferencial matemático.

Informalmente, el hecho que una función f tiene un límite L en el punto p, significa que el valor de f puede ser tan cercano a L como se desee, tomando puntos suficientemente cercanos a p, pero distintos de p.